- videbaks's home page
- Posts
- 2025
- 2024
- 2023
- 2022
- 2021
- 2020
- 2019
- 2018
- December (1)
- November (2)
- October (1)
- September (1)
- August (1)
- July (4)
- April (3)
- March (1)
- February (2)
- January (1)
- 2017
- 2016
- November (1)
- September (2)
- August (2)
- July (1)
- June (1)
- May (1)
- April (1)
- March (1)
- February (1)
- January (1)
- 2015
- 2014
- 2013
- 2012
- 2011
- 2010
- November (3)
- 2009
- My blog
- Post new blog entry
- All blogs
vertex distributions
Updated on Sat, 2019-07-06 17:21. Originally created by videbaks on 2019-07-06 17:21.
There has been extensive discussion of how to optimize the 200 GeV running.
I did a few caculations quantifying this. Some basic
- assume initial vertex distribution is Gaussian with sigma of 50 cm
- assume beam width at z-0 is 150 microns
- The hourglass effect implies that sigma(z)=sigma(0)*sqrt(1+z*z/beta*beta)) where beta is the beta*, nominaly 0.7 m at 200 GeV.
- Assume that the beam have a crossing angle of 0.0, 0.001,0.002 mrad
- Reduction at given Z is reduced by Gaussian dist of width(z) vs. seperation
The results can be seen in the following Graph
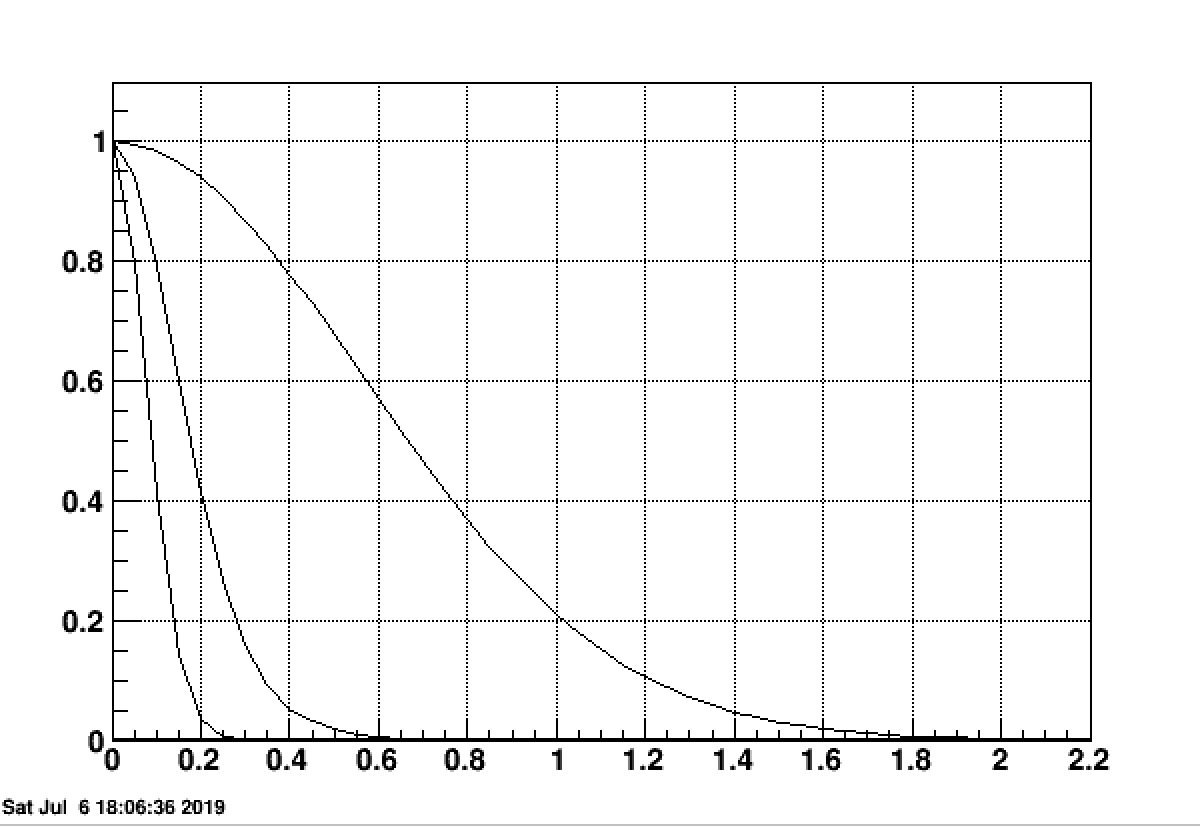
A couple of comments to think about
- The vertex distribution are much narrower with the crossing angle is already pointed out. The luminosity for the reduced widths are 30% for 0001 and 16% at 0.002 of the nominal lumi.
- The intrinsic divergence in the beam has not been considered
- With a crossing angle collisions there is center-of-mass transverse velocity. This will e.g for crossing angle of .002 change the measured pt of pions at 0.5 GeV/c by 1 MeV/c in the plane (+- in opposite hemispheres). This should be acceptable.
- The estimates do not take into account the intrinsic divergence of the beam, so the effective widht may be underestimated.
»
- videbaks's blog
- Login or register to post comments